

 |
Elena A. Ivanova St. Petersburg State Polytechnical University |  |
Example of body-point of general type
Let us consider a body-point the inertia tensors of which are the spherical part of tensors. This body-point is an example of body-point of a general type, the dynamical properties of which differ from the dynamical properties of rigid bodies. The definition of body-point of a general type is the assignment of its kinetic energy. The kinetic energy K of the considered body-point is
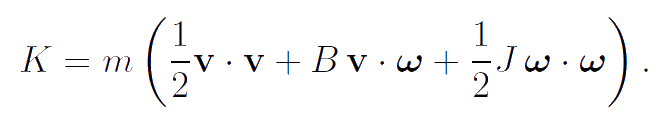 |
Here m is the mass of the body-point, mB and mJ are the moments of inertia. It is important to note that this body-point differs from the infinitesimal rigid body just by the additional parameter B. The momentum K1 of the body-point, its proper angular momentum K2 and the angular momentum calculated with respect to a reference point Q have the form:
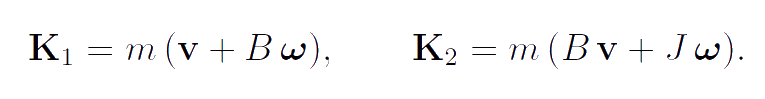 |
The motion of a body-point is described by two Euler's laws of dynamics which are formulates as follows:
The equation of momentum balance. The rate in the momentum change is equal to the force acting on the body-point from its environment.
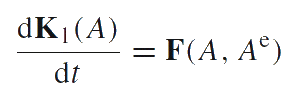 |
The equation of angular momentum balance. The rate in the angular momentum change, calculated with respect to a reference point Q, is equal to the moment acting on the body-point from its environment, calculated with respect to the same reference point Q.
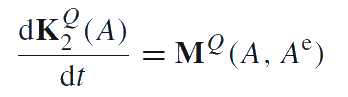 |
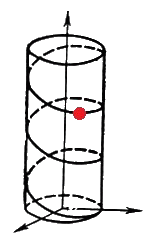 |
The use of the particles of this type provides additional opportunities to account for the mutual influence of mechanical and non-mechanical processes. When modeling elementary particles and the internal structure of atoms these particles can be convenient because they possess the property of dynamic relatedness of translational and rotational motions. As proved by P.A.Zhilin, the free motion of such particle is uniform motion along the helical curve whose axis is directed along the momentum vector (see Figure). Thus, the free motion of this particle is similar to the motion of the charged mass point in a uniform magnetic field. That is why P.A.Zhilin believed that the additional inertial parameter B can be considered as characteristic of property of the particle which is an analogue of the charge, see for example:
Afterwards the particles of this type have been used in order to model the dissipative properties of a thermoviscoelastic medium, see for example:
Thus, constructing model of continuum we can use the body-point of a general kind as the base material object. The body-points of a general kind possess the additional inertia characteristics as compared to the infinitesimal rigid body. Therefore the continual models based on using body-points of a general kind will possess some additional properties as compared to the known continual models. |
To view PDF files you can download free version of Adobe Acrobat Reader.