

 |
Elena A. Ivanova St. Petersburg State Polytechnical University |  |
Dynamics of molecular systems
Control for internal dynamics of molecules can be carried out by many ways. However, one of the most perspective ways consists in influence on molecules by an electromagnetic field, oscillating with the frequencies near to frequencies of oscillations of atoms in molecules. The modern laser technologies allow not only to create such fields, but to change the form and duration of pulses operatively. Frequencies of molecules oscillations lay in infra-red area of a spectrum. The corresponding periods of oscillations for two-atomic molecules are tens of femto-seconds. The most high-speed modern lasers give possibility to create pulses in the same time range, allowing thus to influence a molecule in its real time. Besides, the same laser pulse can be used and for an establishment of a feedback. On change of the pulse past through the molecular medium, it is possible to estimate a condition of system and to correct control influence operatively. Realization of a similar feedback in real molecular time is behind a side of opportunities of modern technical equipment. However it is rather probable, that in the near future it becomes available for quickly developing laser technologies.
Simulation of molecular systems
The problems arising from control for oscillations of molecular systems are substantially similar to problems of control for nonlinear mechanical systems. Nanometer scale level and duration in tens and hundreds of femto-seconds is that area where laws of classical mechanics are applicable. The success of the analysis of a problem of control is defined by a successful choice of mechanical model of a molecule. The first problem which is arising when a researcher attempts to create mechanical model of a multi-atomic molecule is the fact that the pairwise central interaction cannot provide stability of spatial structure and adequately describe frequencies of oscillation of the majority of multi-atomic molecules. Linearly oriented three-atomic molecule is the simplest example illustrating this fact (see figure).
 |
It is obvious, that if potential energy of such molecule depends only on coordinates of its atoms then bending oscillations of the molecule will be essentially nonlinear, and corresponding frequency of small oscillation is equal to zero, that contradicts experimental data. Considerable divergences with experimental data arise as well for three-atomic molecules whose valent corners are distinct from 180 degrees. In particular, it is known, that there are three eigenfrequencies in infra-red area of a spectrum of molecule NO2. The eigenforms of oscillations, corresponding to these eigenfrequencies, are represented in figure.
 |
If only pairwise force interaction is taken into account then the model of a molecule contains two various rigidities. A variation with two rigidities does not give possibility to satisfy to experimentally known values of three eigenfrequencies. The traditional decision of this problem consists in adding into the system of the angular spring creating the moment, proportional to a deviation of a corner between valent bonds from its equilibrium value. It is the elementary example of many-particle interaction. Many-particle potentials of interaction are widely used for the description of molecular systems.
The problems connected with usage of the concept of many-particle interaction
The main lack of many-particle interaction is that after dissociation of molecules this interaction loses sense. The ideology of many-particle interaction means that, for example, in molecule NO2 the law of interaction of atoms N and O (i.e. properties of chemical bond N-O) depends on position of second atom O. Let us consider the process of dissociating of the molecule. Let us suppose that the second atom O comes off (see figure).
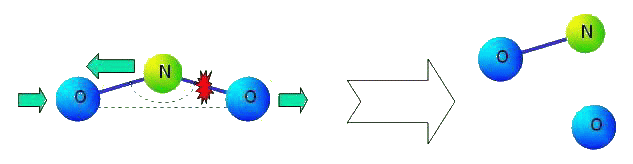 |
What will happen with kept chemical bond N-O? It turns out, that this bond should change its properties essentially. Chemical bond in formed molecule NO can not depend on a former valent corner of molecule NO2 not existing any more. There is also other problem. It is known, that there are three pronounced resonant peaks in infra-red area of a spectrum of molecule NO (see figure).
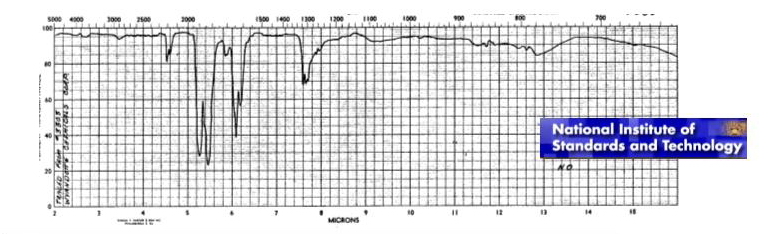 The schedule is published on a web-site of National Institute of Standards and Technology
http://www.nist.gov
The schedule is published on a web-site of National Institute of Standards and Technology
http://www.nist.gov
|
The model based on pairwise central interaction gives possibility to describe only one frequency.
 |
This model, certainly, can be used in calculations. But at least, it is necessary to answer the question on what frequencies from experimentally known ones are corresponded to the model, because value of rigidity of the atomic bond depends on this. It is easy to see, that the first resonant peak is the least and the third one is the greatest. Taking into account this fact it is difficult to prefer one of the frequencies. The concept of many-particle interaction will not help with the decision of the problem, because molecule NO contains only two atoms.
The concept pairwise moment interaction
Introduction of the moment interaction between atoms is the decision of the problems listed above. In this case it is possible to remain in the limits of pairwise (though and not central) interactions. For the large deformations of molecules pairwise moment interaction essentially differs from many-particle one. The main advantage of the moment interaction is that it, being pairwise interaction, completely keeps its sense when molecules are dissociated.
Let us note that in the linear problems corresponding to small deformations of multi-atomic molecules, pairwise moment interaction is equivalent to many-particle interaction in many cases. It will be so, for example, in a problem of linear oscillation near to position of equilibrium of a three-atomic molecule (see figure).
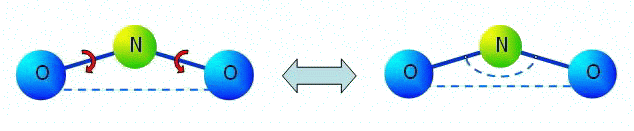 In figure it is denoted:
In figure it is denoted:segments are force interaction, the arc arrows are moment interaction of N-O, dotted arc is an angular spring between bonds N-O in many-particle model. |
Parameters of pairwise moment interaction are determined on experimental data by the same way as parameters of many-particle interaction. Values of rigidities of atomic bonds in molecule NO2 calculated on experimentally known values of three eigenfrequencies of oscillations of this molecule are in the table. In the model under study the moment interaction between atoms N-O, is taken into account but inertia of rotation of atoms is ignored and interaction of atoms O-O is considered only force. This model has three eigenfrequencies. Knowing values of three eigenfrequencies we can find three parameters of rigidity: rigidity on a tension of bond N-O, rigidity on a tension of bond O-O and some combination of cross rigidity and rigidity on turn of bond N-O. This combination has the dimensions of cross rigidity and it is named the resulted cross rigidity.
 |
 |
Three facts seem interesting. 1) The resulted cross rigidity of bond N-O is comparable with tension rigidity. It means that it is important to take into account moment interactions for this molecule. 2) Rigidity of bond O-O is negative. It means that atoms of oxygen repel each other. The last it is no wonder as the distance between atoms of oxygen in molecule NO2 is less, than in molecule O2. 3) Cross rigidity and rigidity on turn can not be determined on experimental values of frequencies. Their combination named resulted cross-section rigidity is determined only. However these data are enough to determine all parameters of nonlinear moment potential of interaction. There is one-to-one conformity between moment and many-particle models. It takes place at the following ratio between their parameters.
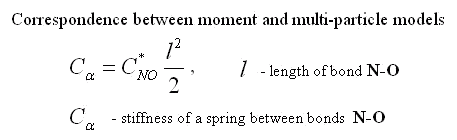 |
Introduction of pairwise moment interaction in addition to pairwise force one is a unique opportunity to describe three frequencies of an infra-red spectrum for two-atomic molecules, in particular, molecule NO (see figure above). As a result of introduction of the moment interaction the force interaction becomes not central and two rigidities (cross rigidity and rigidity on turn) are added in the model. If inertia of atoms on turns is taken into account (i.e. atoms are considered as the particles possessing the nonzero moments of inertia) then two additional oscillatory degrees of freedom appear in the model. One degree of freedom corresponds to relative movement of particles in direction perpendicular to bond. Other degree of freedom corresponds to relative rotation of particles (see figure).
 |
Expressions for eigenfrequencies of the moment model of a two-atomic molecule are represented below. The notations represented in the table above are used for distance between atoms and bond rigidities. Standard notations are used for masses and the moments of inertia .
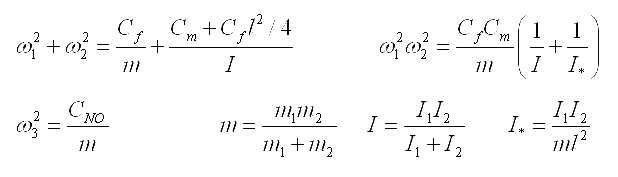 |
Let us note that one of frequencies of the moment model corresponds to longitudinal oscillations and coincides with frequency of the simplest model. Two other frequencies correspond to bending oscillations. These frequencies are expressed in term of the parameters inherent a moment model only. Formulae represented above give possibility to determine rigidities of atomic bonds of the moment model on experimentally known values of eigenfrequencies. There are two problems on this way. The first one is connected to the decision of a question on what frequency corresponds to what oscillations. The second problem is a determination of the moments of inertia of atoms in conditions when their weights and radiuses are known, but there is open a question on the law of distribution of mass in atom. Criterion of correctness of determination of rigidities of atomic bonds can be based on experiments with isotopes (i.e. atoms having various weights and the moments of inertia and identical chemical properties).
Let us note that pairwise moment interaction has the important quantitative advantage with respect to many-particle one. This advantage is caused by that for n-atomic molecule number of the interactions per one atom is proportional n while for three-particle interaction this number is already proportional to n squared.
To view PDF files you can download free version of Adobe Acrobat Reader.