

 |
Elena A. Ivanova St. Petersburg State Polytechnical University |  |
Development of theoretical foundations of particle and molecular dynamics
The method of molecular dynamics consists in the following. The big ensemble of the particles modeling atoms or molecules is considered. The particles interact with each other and besides can be subjected to external influence. In overwhelming majority of cases particles are considered as point masses. For all particles the equations of motion are formulated. The received system of the equations is solved by numerical methods. Rapid development of computer facilities gives possibility to solve such problems for the increasing number of particles. However, now it is impossible to model a macroscopic body, comparing each atom a point mass. That is why when problems of deformation of macroscopic bodies are solved point masses model not atoms or molecules, but larger formations including hundreds and thousands of atoms. In this case the method is usually named a method of particle dynamics though from the mathematical point of view it does not differ from the method of molecular dynamics.
Pairwise potentials of interaction and the Newton's mechanics
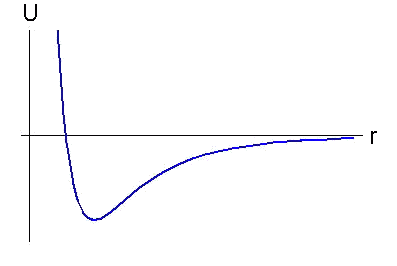 |
Methods of molecular dynamics and particle dynamics are based on Lennard-Jones type pairwise potentials of interaction. The concept of pairwise potential implies that interaction of two particles depends only on their relative positioning and does not depend on position of any other particles. All potentials of Lennard-Jones type describe interaction for which pushing away at small distances and attracting at greater distances are characteristic. These potentials look like, represented in figure. They differ with equilibrium distance, depth and breadth of a potential hole, and also rate of decrease on infinity. Lennard-Jones type potentials enable one to describe the properties of a great number of substances on the qualitative level. It is well known, however, that these potentials have essential drawbacks. One of the major drawbacks is that pairwise potentials can provide stability only for crystal lattices with dense packing. 3D and 2D lattices with lower packing densities (e.g., a simple cubic lattice) are unstable for most of the pairwise potentials. (The case when interactions of all atoms of a lattice are described by means of the same potentials is discussed.) The structures characteristic of covalent crystals - hexagonal lattice on plane (graphite structure) and diamond structure in space - are also unstable. Besides pairwise interaction cannot provide stability of spatial structure and is adequate describe oscillation frequencies of the majority of multi-atomic molecules. |
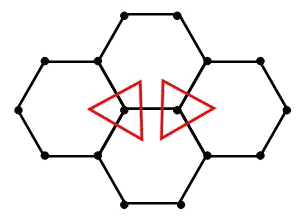
Problems of molecular dynamics in connection with the description of behaviour of crystal lattices, as a rule, are solved within the limits of Newton's mechanics where translational motions and corresponding interactions are considered only. It is meant, that any model of a crystal lattice or a multi-atomic molecule, constructed on the basis of pairwise potentials, represents a design consisting of rods connected among themselves by means of hinges. It is clear, that not everyone such design is stable. Equilibrium state of a hinge design will be indifferent if the deformations not changing length of bonds are possible. Models of lattices with low packing densities, taking into account only valent bonds (i.e., interactions of the nearest atoms), correspond to hinge designs, whose equilibrium state is indifferent. As an example the graphite layer represented in figure can serve.
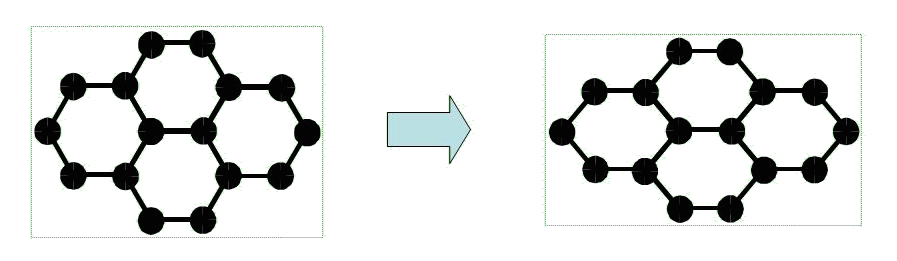 |
Influence of the further next atoms can transform indifferent equilibrium state in unstable one if forces of interaction with the further next atoms will be not returning, and destabilizing. It occurs in models of the majority lattices with low packing densities and multi-atomic molecules as distances between the further next atoms appear on a unstable site of interaction potential. It is obvious, that to solve this problem it is necessary to introduce interactions, obstructing to change of angles between bonds.
Many-particle potentials of interaction
The traditional solution of these problems consists in application of many-particle potentials of interaction. Similar potentials depend on angles between bonds that allow to make stable structures with low packing density and adequately to describe oscillation frequencies of some molecular combinations. The model of a three-atomic molecule represented in figure is an elementary example of many-particle interaction.
 Dotted arc is an angular spring between bonds N-O.
Dotted arc is an angular spring between bonds N-O.
|
Interaction of atoms in this molecule is described by means of three-particle potential and characterized by two parameters of stiffness: stiffness of bond N-O and stiffness of a valent angle. Unfortunately, as a rule, the structure of many-particle potentials appears rather complicated and physical sense of their parameters is not clear. The parameters are calculated from conformity to physical properties of modelled substances. However, at transition from one crystal structure to another (for example, graphite - diamond) it is necessary to change potential of interaction completely. Many-particle potentials of interaction are also widely used for the description of molecular systems. However, often this approach appears especially empirical, requiring selection of the big number of constants, correct only for the concrete chemical combination. Major deficiency of many-particle potentials is that they lose any physical sense at dissociation of molecules and destruction of crystal lattices. Hence the huge class of problems can not be included in area of possible application of these potentials.
Moment interactions in the Euler's mechanics
The alternative approach is based on an idea to take into account moment interaction between atoms. Moment interaction has a clear physical sense and, for this reason, should be preferred to many-particle interaction. We show that by taking into account the pairwise moment interaction (in addition to the pairwise force interaction) one can provide the stability of crystal structures with low packing density. Moment interaction is a reaction to rotational motions. Let us suppose that the atoms are modeled not by point masses, and particles with rotational degrees of freedom, and bonds between atoms possess stiffness on turn. In this case the model of a crystal lattice is not a design constructed by hinge joints. Such model possesses stiffness in relation to any strains. If only valent bonds are taken into account this model will be stable. What will occur to this model of crystal lattice as a result of destabilizing influence of the further next atoms? Before to answer this question, we shall discuss the important difference between force interactions in a system consisting of particle of a general kind and force interactions in a system consisting of point masses.
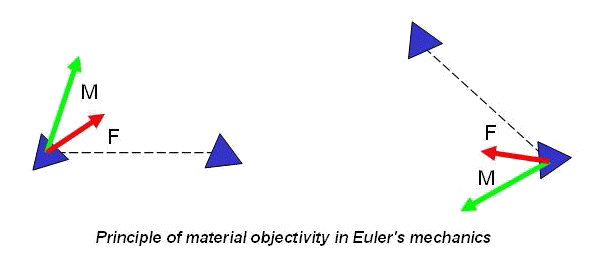
In the Newton's mechanics, considering systems of point masses, forces are central, i.e. directed on a line connecting interacting points. For example, the third law by Newton for point masses looks like, represented in figure at the left.
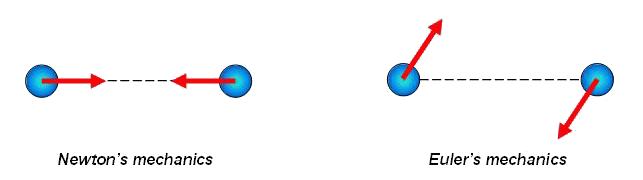 |
In Euler's mechanics, considering systems of particles with rotation degrees of freedom, forces are not obliged to be central. The third law by Newton for particles with rotation degrees of freedom looks like represented in figure on the right. The fact that in Euler's mechanics forces are not central is stipulated by the following. Interaction of particles with rotation degrees of freedom is characterized by pair vectors - a force vector and a moment vector. In general case, the moment vector is not the moment of force, and it is absolutely independent characteristic of interaction. As there are two independent types of a motions - translational motions and rotational (spinorial) motions so there are also two independent types of interactions - force interactions and moment interactions. Thus, in Euler's mechanics, because of presence of the concentrated moments, there exist forces, perpendicular to the lines connecting particles. So, in Euler's mechanics the system of two interacting particles of a general kind can have cross-section stiffness. In the system of point masses it is impossible. More detailed information concerning with Euler's mechanics can be found in the papers by P.A.Zhilin.
Let us return now to a question on a crystal lattice. It is obvious, that instability of crystal lattices is caused by that valent bonds cannot compensate destabilizing influence of other atoms. Cause is the fact that if atoms modeled by point masses then the forces are central and they can create resistance to motions not in all directions. If atoms are modeled by particles of a general kind valent bonds have both longitudinal stiffness and cross-section stiffness and as a result they create resistance to any motions. If longitudinal stiffness and cross-section stiffness of valent bonds appear enough greater, forces of interaction with the nearest atoms will compensate destabilizing influence of the further atoms and the model of a crystal lattice will be stable.
Creation of many-particle potentials is attempt of introduction moment interactions in mechanics of point masses. As point masses cannot perceive moment influence and react to them, it is necessary to introduce into consideration the interactions depending on angles between bonds. Each angle between bonds is defined by position of three atoms. That is why these potentials are named many-particle. Such approach, certainly, is possible, but inconsistent. Therefore, it is no wonder, that many-particle potentials have very complicated structure.
Difficulty of the description of pairwise force and moment interactions
Using of concept of the moment interactions in the pure state in the methods of molecular dynamics and particle dynamics is exotic now. Attempts to consider rotational degrees of freedoms and moment interactions were undertaken for simulation of the granulated medium. However the ideas underlying of these researches were not beyond Newton's mechanics as particles of the finite size were considered and moment interactions were resulted from an integration of the moments of forces distributed on a surface.
Why in overwhelming majority of cases methods of molecular dynamics and particle dynamics are based on Newton's mechanics instead of on Euler's mechanics? This situation takes place in spite of the fact that necessity of the consecutive introduction of the moment interactions is obvious for a long time. The reason, probably, consists in the fact that pairwise force and moment interaction of particles of a general kind cannot be practically described, using only intuitive representations and empirical knowledge. From the theoretical point of view, the description of pairwise interaction of point masses and the description of pairwise interaction of particles of a general kind represent problems of absolutely different level of complexity. Let us explain this statement. In the mechanics of point masses forces are central, therefore for the description of pairwise force interactions the determination only of module of the force vector is required. Thus, according to a principle of material objectivity, force should not vary at a motion of system as the rigid body (see figure).
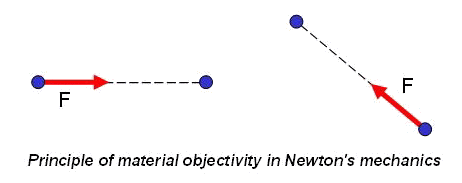 |
Hence, force of interaction of point masses depends only on distance between them. Thus, in case of only force interactions the determination of force is reduced to the determination of one scalar function of one scalar argument. If the rotational degrees of freedom are taken into account interaction of particles is characterized by two vector quantities - a force vector (which is not central in this case) and a moment vector (which also can be arbitrary). A force vector and a moment vector depend, generally speaking, on four vector arguments - position vectors and turn vectors of both interacting particles. According to a principle of material objectivity force and moment vectors should not vary at a motion of system as the rigid body (see figure). Hence, the principle of material objectivity gives possibility to cancel number of arguments, having reduced them to two vector quantities.
 |
So, if the rotational degrees of freedom are taken into account, the description of pairwise interaction of particles demands the determination of two vector quantities in the form of functions of two vector arguments. Such problem is practically inaccessible for human intuition. Fundamental physical ideas and strict mathematical methods are required for its solution. These methods are developed in the mechanics of multipolar media where a stress tensor and a moment stress tensor are defined as partial derivative of an internal energy with respect to strain tensors (Cauchy-Green relations). A method of definition of the strain tensors, based on usage of a special mathematical formulation of the energy balance equation has been suggested and developed in papers by P.A.Zhilin.
The historical information
Historically the method of molecular dynamics has arisen in a molecular physics. In a molecular physics this method has been developed and substantiated. Various potentials of interaction had been suggested by specialists on a molecular physics. Let us notice, that in physics the basic model is the point mass, therefore moment potentials of interaction in the pure state could not arise here. Attempts to consider moment interactions have led to that now is known as many-particle potentials. In connection with problems of solid mechanics a method of molecular dynamics (here already the method of particle dynamics) has started to be used as something completely formulated. For a wide class of problems usage of known potentials of interaction has yielded good results. Probably therefore the method of particle dynamics has not gained serious theoretical development in mechanics. At the same time, in mechanics there are physical ideas and mathematical methods connected with description of moment interactions of particles of a general kind. Moment theories are developed in mechanics during some centuries. Idea to take into account rotational degrees of freedom and moment interactions lays in the foundation of such popular in engineering calculations mechanical models as rods and shells. Modern investigations in this area are connected with creation of various 3D models of continuum mechanics, considering rotational degrees of freedoms and moment interactions. Interest to similar models is caused by that they possess properties, typical, for example, for piezoelectrics or ferromagnetics, i.e. materials in which mechanical strains are directly connected with manifestation of the electrical and magnetic phenomena (see papers by P.A.Zhilin).
Example of moment potential
It is obvious, that the concrete form of moment potential of interaction depends on internal structure of interacting particles. If particles model atoms then description of their internal structure is very complicated problem. However, the geometry of molecular combinations and crystal lattices, which can be formed by these types of atoms, gives possibility to understand what symmetry the particles modelling atoms should possess. For particles which can form a square lattice in a plane, a degree of symmetry is n = 4. For the particles forming a triangular lattice in a plane, a degree of symmetry is n = 6. For the particles forming a graphite layer (see figure), a degree of symmetry is n = 3. So, the degree of symmetry of the particles forming a lattice in a plane is defined by number of valence bonds.
|
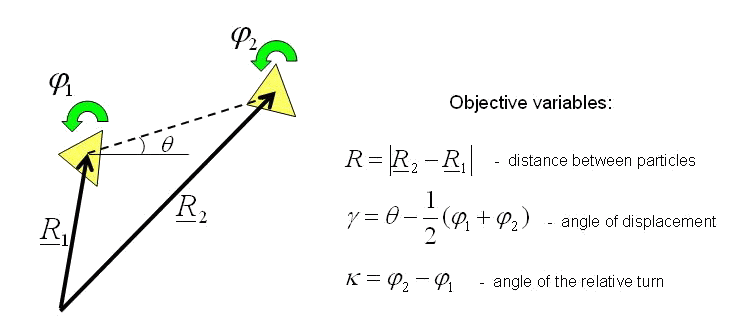
Let us consider system of two interacting particles (see figure). When a system of two particles moves in a plane, the configuration of this system is characterized by three objective variables which are written to the right of figure. Variables, not dependent on moving system as the rigid body, are named objective.
|
The potential of interaction of the identical particles, capable to form a crystal lattice in a plane is formulated below.

|
The detailed information on why moment potential depends from resulted above arguments, instead of from any others, and also how the force vector and the moment vector are calculated by moment potential contains in the publication:
To view PDF files you can download free version of Adobe Acrobat Reader.