

 |
Elena A. Ivanova St. Petersburg State Polytechnical University |  |
Piezoelectrics
There exist many crystals having piezoelectric properties. The piezoelectric properties reveal themselves as a result of the influence of electromagnetic fields on matter. Piezoelectric materials can be divided into two classes: polar and non-polar piezoelectrics. For example, LiGaO2, Li2GeO3, CdTe, BaTiO3, PZT, Pb5Ge3O3 are polar piezoelectrics, and α-HIO3, KH2PO4, TeO2, Bi12GeO20, Bi12SiO20, β-ZnS, α-SiO2 are non-polar piezoelectrics. The qualitative difference of properties of polar and non-polar piezoelectric materials consists in the fact that in contrast to non-polar piezoelectrics the polar piezoelectric materials (ferroelectrics) have non-zero dipole moment unit volume, i. e. they possess spontaneous polarization. However, in the classical theory of piezoelectricity based on the equations of electrostatics and symmetric theory of elasticity there is no qualitative difference between polar and non-polar materials. According to the classical theory the only difference between polar and non-polar materials is that the piezoelectric modules of polar materials are much greater than those of non-polar materials. The objective of our investigation is to describe piezoelectricity taking into account the qualitative peculiarities of polar and non-polar materials. We use the method suggested by P.A.Zhilin. The main ideas of the method are to consider the microstructure of piezoelectric materials and use the equations of micro-polar continuum. Thus, starting from the consideration of microstructure of piezoelectric materials we suggest two theories of piezoelectricity based on the equations of micro-polar continuum. The first theory describes the piezoelectric effect in polar materials. This theory is based on the model of complex particle possessing a non-zero dipole moment. The second theory describes the piezoelectric effect in non-polar materials. This theory is based on the model of unit cell which has a non-zero quadrupole moment and zero dipole moment. Under certain simplifying assumptions both theories can be reduced to the classical theory of piezoelectricity.
Polar piezoelectric materials
 |
The basic idea is to consider the medium with particles that are neutral dipoles. The neutral dipole is a pair of charges q+ = q and q- = - q separated by a distance. The dipole can
move in space and rotate, and also change its value, i. e. it can stretch and compress. The reference position of the dipole (see Figure) is characterized by the following quantities.
Radius-vectors R0+ and R0- determine the positions of charges q+ and q- , correspondingly,
vector l0 determines the relative position of the dipole charges, and radius-vector r0 determines the position of dipole center. When passing to the actual position
the charges q+ and q- move to the points determined by radius-vectors R+ and R-, correspondingly, the dipole center moves to the point
determined by radius-vector r. Vector l determining the relative position of the charges of dipole in the actual configuration is equal to R+ – R-.
The quantities characterizing the displacements of dipole center and dipole charges are determined as u = r – r0,
u+ = R+ – R0+, u- = R- – R0-.
|
We suppose the effect of electric field to be an external action. There are two ways to calculate the power of this external action. On the one hand, the power of external actions per unit volume of continuous medium is equal to the sum of the body force power and the body moment power. On the other hand, we can write the expression for the rate of energy density change due to the influence of electric field on the dipoles. By using the long-wave approximation and the well-known formula for the force acting on a charge F = qE, where E is the electric field vector, after simple transformations, the expression for the rate of energy density change takes the form:
The power of external actions is equal to that part of the rate of energy change which depends on the translational and angular velocities. Consequently, the coefficient of the translational velocity can be associated with a body force ρF, the coefficient of the angular velocity can be associated with a body moment ρL, and the last term can be associated with the quantity Q characterizing the energy supply from an external source:
The detailed description of the suggested theory and a comparison of this theory with the classical theory of piezoelectricity can be found in [1], [2].
Non-polar piezoelectric materials
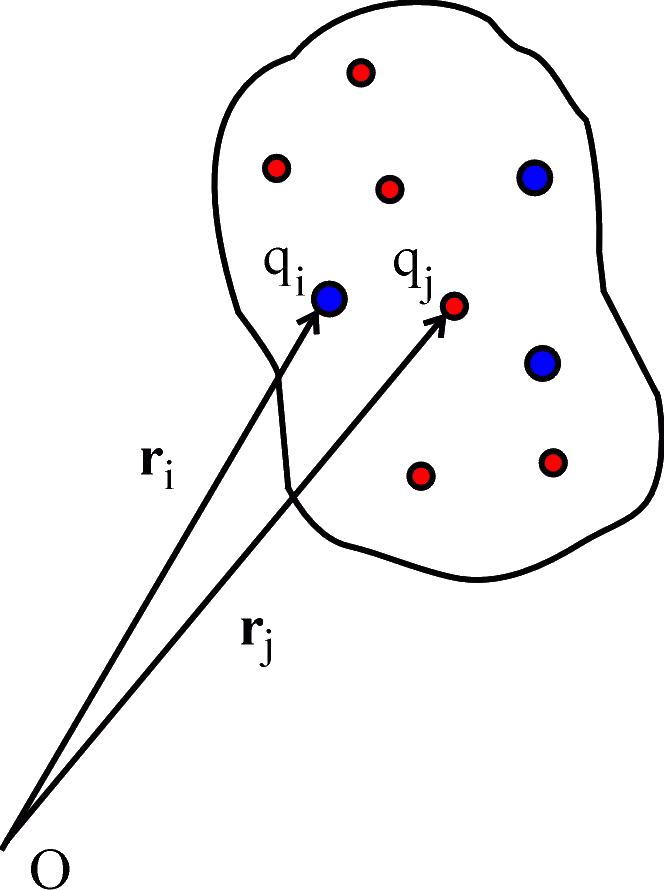 |
We consider the crystal lattice with unit cells consisting of N ions which have charges qi (see Figure). In the reference configuration the position of mass center of cell is determined by the radius-vector r, the positions of ions are determined by the radius-vectors ri = r + bi where the radius-vectors bi determine the positions of ions relative to the mass center of cell. We introduce the electrical characteristics of the unit cell: the total charge q, the dipole moment d and the quadrupole moment Q which are calculated by the formulas:
In crystals the total charge of the unit cell is equal to zero whereas the dipole moment d and the quadrupole moment Q can be zero or nonzero depending on the type of material. It is known that if the total charge and the dipole moment are equal to zero then the quadrupole moment does not depend on the point with respect to which it is calculated. Further, we consider non-polar piezoelectrics, i.e. piezoelectric materials with zero dipole moment. Thus, q = 0, and d = 0. To describe the kinematics of the unit sell we introduce the displacement vectors of ions ui. Further all displacements are supposed to be small and the following representation for the displacement vectors ui and the polarization vector pd are used:
Here u is the displacement vector of center of unit cell, φ is the vector of small rotation of unit cell as a rigid body, ξi are the variables characterizing the deformation of unit cell. We suppose the ion displacements associated with the deformation of the unit cell to be much less than the ion displacements connected with the movement of the cell as a rigid body. In other words, we assume that |ξi| << |u| and |ξi| << |φ × bi|. Note that the formula for the polarization vector pd is valid only in the case of non-polar piezoelectric material, i.e., when q = 0 and d = 0. |
Next, we introduce the volume density of the quadrupole moments being the parameter of the medium, the volume density of piezoelectric polarization being one of the basic variables:
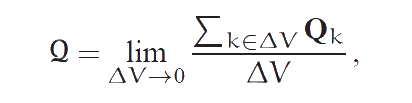
| 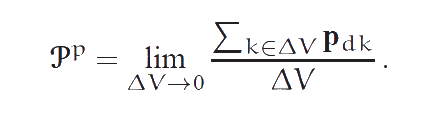 |
We suppose the electric field to be an external factor. Starting from this asumption we prove that the body force ρF, the body moment ρL, and quantity Q characterizing the energy supply from an external source have the form:
The detailed description of the suggested theory and a comparison of this theory with the classical theory of piezoelectricity can be found in [2].
Conclusion
Above two micro-polar theories of piezoelectricity based on the continuum with internal degrees of freedom are considered. One of these theories describes the polar piezoelectric materials, and the other describes the non-polar materials. In contrast to the classical theory where the constitutive equations establish the relations between the electric field vector E and the electric induction vector D, in the suggested micro-polar theories the constitutive equations relate the electric field vector E and the polarization vector Pp. It is proved that under certain simplifying assumptions the suggested theories of piezoelectricity pass into the quasi-classical ones. The quasi-classical theories differ from the classical theory of piezoelectricity by the presence of the additional terms of the piezoelectric nature in the equations of motion and the constitutive equations.
Publications
To view PDF files you can download free version of Adobe Acrobat Reader.