Wiercigroch M., Zhilin P.A. On
the Painleve Paradoxes // Nonlinear Oscillations in Mechanical Systems:
Proc. of the XXVII Summer Schools. St. Petersburg. 2000. P. 1-22.
Dry friction and Painleve paradoxes
The friction is one of the most widespread phenomena in a Nature.
The manifestations of friction are rather diverse. The laws, with
which the friction in concrete situations is described, are
diverse as well. Most popular in the applications are two laws of
friction: the linear law of viscous friction and so-called dry
friction. The viscous friction is well investigated, and its
manifestations are clear and are easily predicted. It cannot be
said about the laws of dry friction, though they are studied and
are used in practice already more than two hundred years. Note
that the friction, arising at sliding of one rigid body on another
at absence of greasing, is called the dry friction. The relative
sliding of bodies in contact, as a rule, is accompanied by
occurrence of forces of friction, which render significant
influence on dynamic processes in different sorts technical
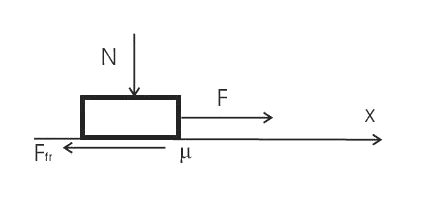
devices. Coulomb carried out the first researches of the dry
friction in the end of XVIII century. The schematic of the Coulomb
experiment is submitted in a Figure.
In 1791 Coulomb has published the first formulation of the law of dry friction
in the following simple form.
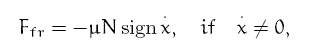The external simplicity of this law rather deceptive. As a matter of fact the
Coulomb law of friction is the most complicated constitutive equation in
mechanics. This may be seen, for example, from the fact that up to now the
general mathematical statement of the Coulomb law of friction is absent in
literature. The formulation is only small part of general statement. In
experiments by Coulomb the force of squeezing N of bodies was set and was
known. However, this force is not known in the most of nontrivial problems and
must be found in the process of a solution of the considered task. In some
cases, the function N(t) can have complex view and depends on many
physical features of the task under consideration. Factor of friction μ is
accepted to be the characteristic of bodies in contact. Now factors of
friction for various pairs of bodies are resulted in the data books.
In the simple situations the Coulomb law allows completely to solve the put task.
During about one century it was considered, that the Coulomb law does not
comprise any ambiguities from the theoretical point of view. At the same time,
the rough development of machine-tool construction in second half of XIX
century has revealed many cases, in which, on the first sight, the application
of the Coulomb law leads to some contradictions. The special anxiety was
caused by strange vibrations of machine tools (in some decades they were
investigated and have received the name of frictional
self-oscillations), processing, sharply lowering accuracy, of let
out products. Sometimes the character of the movements arising in
certain conditions was very strange, almost saltatory. Now such
saltatory movements became object of intensive researches.
These circumstances, and also the theoretical
needs, have forced the researchers again to address to the Coulomb
law of dry friction.
 |
|
| P.Painleve |
In 1895 Painleve has published the controversial book.
In what follows we shall cite the book “Lectures on Friction”,
which contain other important works on the subject. In a paper by Painleve the
opinion was expressed, that the Coulomb law is incompatible to the
basic principles of the mechanics. Analyzing numerous examples of
application of the Coulomb law in tasks of dynamics of systems
with friction, Painleve comes to completely unexpected conclusion:
“... While the marked special conditions are carried out, law by
Coulomb is in the contradiction with dynamics of rigid bodies”
and further “...Between dynamics of a rigid body and the Coulomb law
there is a logic contradiction under conditions, which can be carried out in the
reality”. As the logic a contradiction
Painleve names situations, when the solution of the basic task of
dynamics either does not exist, or is not unique. In modern
literature these contradiction are known as the Painleve
paradoxes.
Now conclusions by Painleve even if they would be
completely correct already anybody would not surprise. In
continuum mechanics there is a chapter devoted to the theory of
the constitutive equations, where the basic problem is the
statement of conditions, at which those or other constitutive
equations lead to the correctly put tasks.
The Coulomb law is the
typical constitutive equation, which, basically, can appear
unacceptable. The merit of Painleve consists that he was the first
who has pointed out at this central problem in mechanics. The
Painleve results have called forth long discussion, in which such
scientists as L. Prandtl, F. Klein, R. Von Mises, G. Hamel, L.
Lecornu, de Sparre, F. Pfeifer and, of course, P. Painleve have
taken part. The opinions of the participants of discussion were
separated.
 |
|
| Coulomb |
L. Lecornu, in essence, having
recognized presence of paradoxes, offers to refuse from the model
of rigid body. F. Klein has come to a conclusion:
“The Coulomb law of friction is not in the contradiction neither
with principles of mechanics, nor with the phenomena observable in
a nature: they need only correctly to be interpreted ”. An
originality of results by F. Klein is caused by that he for the
first time in tasks of a considered type used “hypothesis” of
the instant stopping. In this occasion the discussion has found
new features, and at its center there was a hypothesis of F.
Klein, which F. Klein did not consider as a hypothesis, but also
has not deduced it on a level of a fact in evidence. R. Von Mises
concerning a hypothesis of F. Klein has expressed so:
“1. F. Klein explains the phenomenon not from the point of view
of the Coulomb law, but using a new rule obtained from experience.
2. This new skilled rule can be represented in the form of some
modification of the Coulomb law”.
Further R. Von Mises results
rather interesting reasons and gives the formulation adding the
Coulomb law and allowing to combine sights of Painleve and Klein.
Nevertheless, final conclusion by R. Von Mises is those: “Thus,
not logic, but the methodology of the Newton mechanics compels us
to refuse from the Coulomb law”. G. Hamel has joined
the point of view by L. Lecornu about failure of the rigid body
model. L. Prandtl has expressed rather definitely:
“In the statements of Mises and Hamel the speech goes about” to
a hypothesis “of instant stopping. As opposed to this I
emphasize, that in this case it is possible to speak only about
result obtained through limiting transition. The research of
elastic systems shows, generally speaking, something greater: it
may be established, that from two possible movements, which the
conventional theory gives for positive pulses, one, namely,
accelerated motion will be steady, and another, slowed down, will
be, on the contrary, unstable. In a limit we obtain the
indefinitely large instability. So it is quietly possible to tell,
that this second movement is practically impossible. From this it
follows, that it is impossible by no means to expose of logic
doubts against the Coulomb law”. Under the Prandtl offer, F.
Pfeifer made the large research. However, the clear
confirmation of such point of view was not carried out. Thus, in
discussion the Painleve position has not found a convincing
refutation, as was marked in three notes by Painleve
during the discussion. Even those authors, which
disagree with the Painleve position, have not specified in which
items of the Painleve reasoning is mistaken, and, hence, the
position of Painleve remains not challenged. There was an opinion,
which P. Appell has expressed in the
following words: “it is not necessary to think, that only in
exclusive cases there can be possible such difficulties. On the
contrary, they arise in the most common cases, at least, at enough
large value of factor of friction μ. Because of this new
experiments for a finding of the laws of friction, which is not
resulting more in these difficulties, are necessary“.
Nevertheless, some ways of an exit from paradoxical situations
were shown. The basic way of an exit is refusal of the rigid body
model. Other way is application if necessary “hypotheses” of the
instant stopping. However, its substantiation remained behind
frameworks of the carried out researches. For decades, past from
time of end of discussion, the interest to the Painleve paradoxes
that faded, again grew. N.V. Butenin showed
fruitfulness of the Klein hypothesis in the large work. The
significant development of ideas connected to partial refusal of
the rigid body model was made in works of Le Suan Anh,
in which the references to many other works can be found.
 |
|
| F.Klein |
From told follows that it is necessary, firstly, to show features
of the Coulomb law of friction, not complicated by any other
circumstances, and, secondly, it is necessary to consider those
conditions, which were investigated by Painleve. Only after that
it will be possible either to recognize a position by Painleve, or
to reject it partially or completely. It is well known that the
tasks with the Coulomb friction have the not unique solution even
in the elementary cases. F. Klein marked the importance of this
fact for the first time. Namely, F. Klein has found out the
existence of discontinues solutions, which should be taken into
account for avoidance of the Painleve paradoxes. However majority
of the scientists have not accepted the result of F. Klein. It is
easy to understand the main reason of this. In the offer by Klein
we deal with instant stopping of a body of nonzero weight. It is
well known, that in such a case it is necessary to apply the
infinitely large force, what is impossible in a reality. In works
by L.Lecornu and Le Suan Anh
the physical sense of the discontinues solutions
was shown and is specified as to choose the necessary solution
from two possible ones. Nevertheless, as it became clear from the
subsequent discussions, there is a necessity to consider the
solution by F. Klein more carefully.
In given paper the authors are going to show the following. The authors agree
that the laws of dry friction, similarly to all experimentally established
laws, require the further researches and specifications. It is necessary, for
example, if we wish to construct the satisfactory theory of frictional auto
vibrations. At the same time, the authors resolutely object to the established
opinion that the law of friction by Coulomb is the reason of certain
paradoxical results contradicting to the experimental facts or common sense.
If to consider cases, known in the literatures under the name of the Painleve
paradoxes, then it is easy to see that all of them concern to dynamic tasks
for systems of rigid bodies. It is well known that these tasks very frequently
appear incorrectly put, though the law of friction by Coulomb in them can not
be applied. Nonuniqueness or nonexisting of the solution are typical
manifestations of the incorrectly put tasks. If we want to work with rigid
bodies, we should be ready that the not unique solutions can appear which, in
addition, can be non-smooth. The question, hence, consists not in getting rid
of them, but in giving them correct interpretation. The significant part of
given paper is devoted to this. Let's note, that in tasks of dynamics of
systems with the Coulomb friction frequently shows features, characteristic
for dynamics of systems at shock loading. Sometimes this shock loading appears
larvae. Let's show told on an example of a task shown in a Figure. We assume,
that the body moved at t<0 with constant speed. At the moment of time t=0
all active forces stop the action, and the body goes on inertia. Actually at
t=0 occurs shock loading of a body by force of friction. Really, at t<0 on a
body any forces did not act, as the active force was counterbalanced by force
of friction. When the active force has disappeared, the shock loading of a
body by force of friction has taken place. In other words, the collision of
rigid bodies has taken place at absence of seen attributes of impact.
