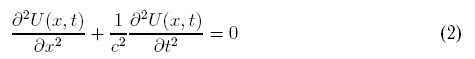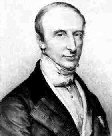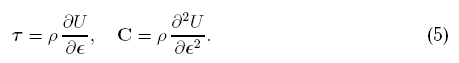Рациональная и экспериментальная механика

Жилин П.А. Основные уравнения теории неупругих сред // Труды XXVIII летней школы “Актуальные проблемы механики”, Санкт-Петербург, 2001. С.14-58.

Рациональная и экспериментальная механика

Я.Бернулли

Механика сплошных сред является объектом пристального внимания исследователей в течение нескольких столетий. Именно в этой области знания зародился анализ, теория дифференциальных уравнений, вариационное исчисление и многое другое. Первое дифференциальное уравнение в истории науки было установлено Я. Бернулли (1694) при изучении равновесия гибких нитей. Оно имеет вид

Уравнение поперечных колебаний струны (Ж.Даламбер, 1749) formI2

Л.Эйлер

и уравнения движения идеальной жидкости (Л. Эйлер, 1755), которые приведены в следующем пункте, явились первыми примерами уравнений с частными производными. С этого времени началось интенсивное исследование поведения твердых деформируемых тел при воздействии на них внешней нагрузкой, а также изучение динамических проблем. Сначала это были тонкие упругие стержни. В 1771 году Л. Эйлер впервые вывел уравнения равновесия тонких стержней

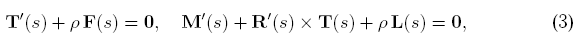независящие от частных свойств материала. Линейная теория упругости была построена О. Коши (1822) и остается неизменной вплоть до наших дней.

О.Коши

История ее создания весьма показательна. В 1821 году О. Коши был рецензентом работы А. Навье, в которой на основе корпускулярных представлений впервые были выведены уравнения линейной теории упругости с одной упругой постоянной. Коши отнесся к этой работе весьма критически, в результате чего работа Навье была опубликована только в 1827 году. Для построения теории упругости Коши выбирает другой подход, ставший основным в механике твердых деформируемых тел. Он вводит понятие упругого континуума, строит теорию напряжений и деформации для этого континуума, постулирует линейную зависимость тензора напряжений от тензора деформаций и выводит уравнения равновесия. Результирующая система уравнений Коши

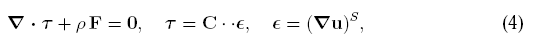где тензор четвертого ранга C называется тензором упругости. Построение линейной теории упругости было выполнено О. Коши за считанные месяцы. После чего в течение следующих 15 лет, вплоть до 1837 года, Коши пытался улучшить построения А. Навье. Этой же проблеме вывода уравнений теории упругости из корпускулярных представлений были посвящены многолетние исследования С.Д. Пуассона. Результаты оказались мало удовлетворительными. Указанное обстоятельство весьма наглядно демонстрирует силу методов механики сплошных сред. Между тем, единственное важное дополнение к теории Коши было сделано Дж. Грином (1839), которое состояло во введении понятия энергии деформации U и постулировании уравнения баланса энергии. 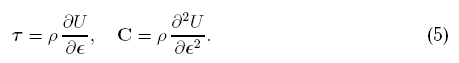Так были получены соотношения Коши-Грина formI5 (2K)

Все сказанное выше хорошо известно и преследовало цель подчеркнуть важный для целей данной работы факт. А именно, со времени вывода уравнений (1) - (5) прошел огромный промежуток времени, в течение которого наши представления о природе сущего радикально изменились. Тем не менее, указанные уравнения сохранили свой вид без каких-либо, даже самых минимальных, изменений. Способность механики сплошных сред строить уравнения, истинность которых не опровергается временем и которые не требуют уточнений, является ее важнейшим достоинством. Последующее развитие механики дополнило, но не изменило, эти уравнения. Здесь уместно обсудить еще один важный исторический факт. После вывода уравнения (1) Я. Бернулли, вплоть до своей смерти в 1705 году, безуспешно пытался вывести уравнение изгиба стержня, т.е. второе уравнение в системе (3). Эта задача, как бы по наследству, перешла к Л. Эйлеру. Сверхгению Эйлера понадобилось почти полстолетия, чтобы выяснить истинную причину неудачи гениального Я. Бернулли. А именно, в 1771 году Л. Эйлер окончательно установил, что ньютоновская механика принципиально неполна. Заметим, что ньютоновская механика - это механика трансляционных движений, управление которыми осуществляется силами. Но в Природе существует еще один тип движения (спинорное движение), которое не сводится к трансляционному. Соответственно, наряду с силами, в механике необходимо рассматривать еще один тип воздействий, а именно моменты, которые в общем случае не сводятся к понятию момента силы. Поэтому в механике, помимо уравнения баланса сил, необходимо постулировать еще один закон — уравнение баланса моментов. Собственно, этот закон был открыт еще Архимедом в форме принципа рычага.

Ж.Лагранж

Известно множество попыток доказать принцип рычага на основе уравнения баланса сил. Видимо, последняя попытка такого рода была предпринята Лагранжем уже после смерти Эйлера. Лагранж полагал, что ему удалось доказать принцип рычага. Отсюда следовало, что уравнение баланса моментов может быть доказано в ньютоновской механике. Поэтому нет нужды выдвигать дополнительный постулат. Эта ошибка Лагранжа задержала развитие механики, по крайней мере, на столетие и вызвала глубокие негативные последствия в современной теоретической физике. Возвращаясь к Л. Эйлеру, отмечаем, что в не вполне осознанной форме Эйлер использовал уравнение баланса моментов еще раньше, при выводе уравнений динамики твердого тела. Примерно так же поступали многие исследователи при использовании принципа рычага, в правильности которого, разумеется, никто не сомневался. Однако в теории стержней подобный прием не срабатывал. Напомним, что в то время теория напряжений в трехмерных средах еще не существовала. Стержень рассматривался, как упругая линия, лишенная толщины. Поэтому ввести момент M как момент силы было невозможно, и его пришлось ввести как самостоятельную сущность. В 1776 году Л. Эйлер дает окончательную формулировку фундаментальных законов механики в виде двух независимых постулатов: законов динамики Эйлера. Только в начале XX-го века спинорные движения вновь получили признание, а эйлерова механика стала интенсивно развиваться только в последние 50 лет. XIX-й век отметился формулировкой еще двух фундаментальных законов, получивших названия первого и второго законов термодинамики. Первый закон термодинамики или уравнение баланса энергии был сформулирован Дж. Грином в 1839 году и уже упоминался выше. Второй закон термодинамики или неравенство производства энтропии рождался в великих муках, имел множество формулировок и, наконец, утвердился в механике сплошных сред в форме неравенства Клаузиуса-Дюгема-Трусделла. Два закона динамики Эйлера и два начала термодинамики составили каркас, внутри которого и строится современная механика сплошных сред. Важно подчеркнуть, что упомянутый каркас не определяет конкретных моделей сплошных сред, поскольку дает незамкнутую систему уравнений. Создание модели сплошной среды равносильно решению проблемы замыкания указанной выше системы уравнений. Иными словами, создание модели сплошной среды равносильно написанию неких дополнительных уравнений, которые принято называть определяющими и которые устанавливают связи между основными переменными, входящими в фундаментальные законы. Долгое время считалось, что установление определяющих уравнений является задачей экспериментальной механики. Это правильно в том смысле, что эксперимент является неустранимым звеном при построении определяющих уравнений конкретных материалов. Тем не менее, в настоящее время уже ясно, что построение определяющих уравнений является теоретической проблемой, которая принципиально не может быть решена методами экспериментальной механики. К обсуждению этого вопроса мы еще неоднократно будем обращаться в дальнейшем тексте статьи. В настоящее время проблема замыкания удовлетворительно решена только для так называемых нелинейно упругих сред, а теория нелинейно упругих сред обрела практически каноническую форму. Существуют материалы, которые удивительно хорошо моделируются нелинейно упругой средой в достаточно широком интервале деформаций. Однако этот класс материалов весьма узок. Большинство реальных материалов, хотя и проявляют свойство упругости, но демонстрируют явное отклонение от того, что принято называть упругостью. Поэтому основные проблемы механики деформируемых тел в настоящее время сконцентрированы в области неупругого поведения материалов. Несмотря на то, что здесь накоплен огромный экспериментальный материал и опубликованы тысячи теоретических работ, тем не менее итоговые достижения в этой области оставляют желать много лучшего. Об этом свидельствуют, в частности, и постоянно появляющиеся новые публикации, содержащие попытки улучшить основы существующих теорий. Ничего подобного не наблюдается в нелинейной теории упругости, где усилия исследователей направлены исключительно на решение конкретных проблем, не меняющих основ теории, но углубляющих и расширяющих результативную часть теории. В чем же состоит главная причина столь разительных отличий между двумя родственными теориями? По мнению автора, основная причина заключается в том, что в теории неупругих материалов телега поставлена впереди лошади. А именно, в нелинейной теории упругости ведущая роль принадлежит сугубо теоретической идее гладкого дифференцируемого многообразия. Эта идея принципиально не может вытекать из эксперимента. Иными словами, сначала лошадь (теоретическая идея и ее реализации), а затем телега с добром (конкретными результатами, уточняющимися и проверяющимися экспериментом). В теории неупругих материалов теоретические модели пытаются вывести из экспериментальных фактов. При этом отсутствует общая теоретическая концепция. Известно, например, что при достаточно больших напряжениях всякий материал обретает свойство текучести, и это свойство закладывается в определение теоретической модели в виде критерия текучести. Но что является причиной текучести и что, собственно, называется текучестью, не обсуждается. Не обсуждается также и определение исходного объекта: от модели сплошной среды в виде гладкого дифференцируемого многообразия приходится отказываться, но никакой замены этому не предлагается. Между тем, отказ от идеи гладкого дифференцируемого многообразия по необходимости влечет за собой отказ от традиционного понимания концепции определяющих уравнений, чего в существующих теориях упруго-пластических материалов не происходит. Напротив, именно на определяющие уравнения в их традиционной трактовке возлагается вся ответственность за основные свойства предлагаемых к рассмотрению теорий.