О прямых подходах к построению теории оболочек

Жилин П.А. Прикладная механика. Основы теории оболочек. СПб: Изд-во СПбГПУ. 2006. 167 с.

О прямых подходах к построению теории оболочек

Л.Эйлер

Прямыми условимся называть подходы, основанные на применении законов механики к абстрактной сплошной среде. Примеры использования прямых подходов доставляют: теория Бернулли гибких нитей, теория стержней Эйлера, теория упругости Коши-Грина, теория изгиба пластин Лагранжа-Жермен. При прямых подходах вопросы обоснования получаемых уравнений остаются в стороне и должны решаться отдельно, что является весьма сложной проблемой. Например, классическая теория упругости обоснована только экспериментально; область ее применимости очерчена по-существу, только на интуитивном уровне. В то же время теория стержней и классическая теория оболочек типа Лява обоснованы с позиций трехмерной теории упругости. Конечно, было бы хорошо, если бы все варианты теории оболочек, необходимые для прикладных целей, можно было бы вывести из трехмерной теории упругости. Но это невозможно по двум основным причинам. Первая: многие полезные прикладные теории оболочек, видимо, нельзя обосновать из-за отсутствия критериев достоверности; некоторые характеристики таких теорий приближенно совпадают с трехмерными, другие же характеристики даже качественно не совпадают с трехмерными. Вторая: во многих случаях, исследуемых с позиций теории оболочек, трехмерная теория вообще отсутствует. Такова, например, теория мягких (из тканей) оболочек или теория биологических мембран. К этому же классу оболочек относятся случаи, когда поверхностная энергия становится сравнимой с объемной энергией (разного рода пленки, включая пьезоэлектрические пленки).

После создания теории упругости первой работой, в которой рассматривались теории стержней, пластин и оболочек и трехмерные сплошные среды с позиций прямого подхода, была книга Е. и Ф. Коссера (1909). Долгое время подхода Коссера выпадал из поля зрения исследователей. Однако, начиная с работы К. Трусделла и Дж. Эриксена (1958), этот подход начал интенсивное развиваться, главным образом, в работах зарубежных исследователей. В России подобные работы не проводились и, по мнению автора, это не очень хорошо. Дела даже не в полезности той или иной теории — заранее это предсказать невозможно. Просто отечественная наука не может позволить себе сильного отставания в какой-бы то ни было области. Мы не будем описывать всех достижений Коссера и их последователей, хотя здесь и получены важные результаты, поскольку этот подхода в данной работе не используется. Опишем коротко только основную идею. Коссера вводят в рассмотрение упругий континуум, каждая тело-точка которого может испытывать смещения и независимые повороты. Упругий континуум может быть одномерным (стержни), двумерным (оболочки) или трехмерным (континуум Коссера). Далее в рассмотрение вводится функционал евклидова действия (действия по Гамильтону), который определен на множестве векторов смещений и поворотов. Основные уравнения выводятся из условий стационарности этого функционала. С теоретической точки зрения подход Коссера, хотя и ограничен, но логически безупречен. В конце шестидесятых годов автор данной работы находился под сильным влиянием этой теории, старательно ее изучал и все же, в конце концов, отказался от нее. Причина была в том, что эту теорию на самом деле очень непросто использовать в прикладных целях. Конечно, когда ответ заранее известен, то нетрудно подобрать соответствующий функционал, но этого недостаточно. Имеются и другие трудности. В теории Коссера “усилия” и “моменты” определяются как производные от лагранжиана и оказываются отличными от настоящих усилий и моментов, с которыми привык иметь дело инженер-расчетчик. Далее, вариационная постановка имеет много достоинств, но имеет и недостатки, связанные с использованием энергии. Конечно, в теоретическом отношении здесь нет никаких проблем, однако в прикладном плане эти проблемы весьма существенны. Дело в том, что функционал энергии крайне критичен к скрытым неконсервативностям, неучтенным потерям энергии и т.д.

Приведем одну школьную задачу: на абсолютно гладкой поверхности лежит свернутая в "комочек" цепь с погонной плотностью ρ затем конец этой цепи начинают вытягивать с постоянной скоростью v так, что все большая часть цепи приходит в движение (“комочек” остается неподвижным); спрашивается, какая сила должна быть приложена к концу цепи?

Решение I: Первый закон динамики Эйлера

где s - длина вытянутой части цепи.

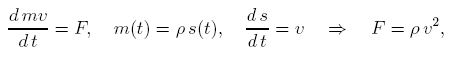
Решение II: Уравнение баланса энергии

Для силы F получили разные ответы. Правильные ответ дает первый закон динамики. При втором же подходе надо искать скрытые утечки энергии. Конечно, они всегда находятся, но не всегда ясно, что их надо искать.

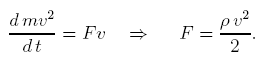
Автор мог бы назвать и современные работы по теории пластин, где допущены ошибки аналогичного типа.

Обратимся к теории оболочек и рассмотрим энергетический (вариационный) подход. Часто поступают так.

Берут энергию трехмерного тела. Затем ее осредняют тем или иным способом и получают двумерный функционал энергии; последняя приписывается оболочке. Верно ли это? Нет, не верно Это будет верно только тогда, когда допустимо использовать гипотезы Кирхгофа-Лява., ибо трехмерная энергия учитывает энергию тех движений частиц оболочки, — трехмерного тела, которые никак не сказываются на движении собственно двумерной оболочки. В то же время законы динамики Эйлера совершенно не чувствительны к подобного рода обстоятельствам. Вспомним, что уравнения движения оболочки могут быть получены из трехмерных уравнений движений посредством вполне точных операций осреднения.

Сказанное ни в коем случае нельзя воспринимать, как критику подхода Коссера. По мнению автора, работа Коссера внесла выдающийся вклад в механику деформируемой среды и ее полезность уже доказана в многочисленных работах. Просто ее приложение к техническим задачам требует известной осторожности, а у инженера зачастую не времени для обдумывания всех аспектов задачи: он выделяет главное и работает только с ним. Поэтому нужны гарантии, доставляемые законами динамики Эйлера.

В целом подход Коссера означает радикальный отход от генеральной линии Бернулли-Эйлера-Коши. В данной работе автор предпочел вернуться к этой линии. А именно, ввести в рассмотрение абстрактный двумерный континуум, наделить его подходящими свойствами и применить к нему основные законы механики. Аналогичный подход, в более ограниченной постановке, используется в последних работах Э.Рейсснера, где рассматривается только статика и, по-существу, не затрагивается решение основной проблемы - формулировки соотношений упругости.

Ознакомиться с развитием теории Коссера можно по работам, содержащимся в списке литературы, и по обзору П.М.Нахди.