Сайт П.А.Жилина

Жилин П.А. Реальность и механика // Труды XXIII летней школы “Анализ и синтез нелинейных механических колебательных систем”, Санкт-Петербург, 1996. С.6-49.

Механика — это не теория какого бы то ни было явления Природы, но метод исследования Природы. В основах механики нет ни одного закона, который хотя бы в принципе мог быть опровергнут экспериментально. В фундаменте механики лежат логические утверждения, выражающие условия баланса неких величин и которые сами по себе не достаточны для построения замкнутых теорий. Для этого необходимо привлекать дополнительные законы, типа закона всемирного тяготения, рассматриваемые как экспериментально установленные факты. Эти дополнительные законы могут оказаться недостаточными или даже ошибочными, но отказ от них не влияет на метод механики. Упомянутая незамкнутость механики может, конечно, восприниматься как ее недостаток людьми, которые полагают, что человечество близко к конечному познанию Мироздания. Те же, кто способен увидеть Реальность, понимают, как бесконечно далеки люди от возможности правильно описать даже относительно простые проявления Реальности. Поэтому корректный метод изучения Природы по необходимости должен включать в себя заранее неопределенные элементы, манипулируя которыми можно улучшать те или иные теории разного рода явлений и тем самым расширять наши представления о Реальности. Механика устанавливает определенные ограничения на допустимую структуру этих неопределенных элементов, но сохраняет в них достаточно широкий произвол.

После этих кратких замечаний о методе механики полезно сравнить современные позиции механики и новейшей физики, возникшие через 70 лет после объявления физикой о “решительном разрыве с классической механикой”.

Системы отсчета. Это краеугольное понятие в механике характеризуется К.Трусделлом как “чистый холст, на котором можно рисовать картины Природы.

А.Пуанкаре

Этот холст должен быть выбран художником прежде, чем он примется за работу. Холст накладывает некоторые ограничения на искусство художника, но никоим образом не определяет те картины, которые художник будет рисовать“. Аналогичный взгляд отстаивал А.Пуанкаре. Прямое несогласие с этой позицией высказывает А.Эйнштейн.

А.Эйнштейн

Например, он пишет: “теория вводит два рода физических предметов, а именно: 1) масштабы и часы (т.е. системы отсчета. П.Ж.), 2) все остальное, например, электромагнитное поле, материальную точку и т.д.” Это в известном смысле нелогично; собственно говоря, теорию масштабов и часов следовало бы выводить из решений основных уравнений, а не считать ее независимой от них. Иными словами, согласно А.Эйнштейну, нужно сначала нарисовать картину, а только потом подбирать для нее холст. Именно так и поступают в общей теории относительности, причем смысл координат, включающих и время, остается принципиально неопределенным.

Как видим, взгляды механики и новейшей физики по этому пункту диаметрально противоположны и несовместимы.

Принцип инерции Галилея (GPI).

Г.Галилей

В механике GPI принимается безоговорочно и отказ от него разрушает все здание механики. Принятие GPI позволяет ввести в рассмотрение инерциальные системы отсчета. Жаль, что этот факт был окончательно осознан и введен в формальные структуры только к 1940г. Однако на интуитивном уровне он принимался в механике с 1638г. Так что логические основы механики были укреплены, но сущностное тело механики менять не пришлось. С концепциями новейшей физики GPI принципиально не совместим, ибо он впрямую противоречит специальной теории относительности. Отсюда ясно, что отвергается в физике и понятие инерциальной системы отсчета. Вместе с тем, А.Эйнштейн и за ним остальные физики используют понятие неускоренной системы отсчета, не определяя этого понятия, т.е. ИСО все-таки вводятся. Не следует думать, что это просто упущение. Такова действительно необходимая для новейшей физики постановка вопроса, ибо GPI впрямую противоречит принципу относительности, основанному на преобразовании Лоренца, а обойтись без привлечения неускоренных систем отсчета не удается.

Равномерность хода времени. И.Ньютон был первым, кто попытался дать определение понятия времени, причем он просто постулировал равномерность хода времени.

И.Ньютон

Как определить понятие равномерности Ньютон не указал, но предположил, что в Природе имеются процессы, позволяющие это сделать. Ниже в п.3 мы еще вернемся к этому вопросу. Детальному обсуждению понятие времени было подвергнуто А.Пуанкаре в 1898г. Основной вывод А.Пуанкаре гласит: “Не существует абсолютного времени; утверждение, что два промежутка времени равны, само по себе не имеет смысла и можно применять его только условно”. Этот вывод обоснован А.Пуанкаре весьма обстоятельно, но, к сожалению, А.Пуанкаре в принципе неправильно понимал GPI и возводил его в ранг физического закона, причем необоснованного (еще одно условное соглашение). На самом деле это не так, что и было показано С.Зарембой, но это важное событие произошло только в 1940г. Если принять GPI, то время в механике вводится с точностью до линейного преобразования t → kt + t₀. Важно подчеркнуть, что формальное обоснование равномерности хода времени в механике с практической точки зрения ровным счетом ничего не изменило в ней, т.к. при этом не изменилось ни одного закона и ни одного уравнения. А вот новейшей физике упомянутое обоснование наносит невосполнимый логический урон. В новейшей физике требование равномерности хода времени игнорируется и подменяется рассуждениями о синхронизации часов в разных точках системы отсчета. Однако эти рассуждения не имеют отношения к требованию равномерности хода времени. Как бы ни синхронизировали часы, но, прежде всего, они должны идти равномерно. В противном случае такие понятия, как скорость и ускорение вообще теряют объективный смысл. Таким образом, и в этом пункте механика и новейшая физика не могут быть приведены в соответствие друг с другом.

Принцип относительности. В механике этот принцип выполняется автоматически. Если в какой-либо теории он не выполняется, то такая теория заведомо содержит ошибки. Никакой существенно новой информации из применения принципа относительности в механике извлечь не удается. Это и не удивительно, ибо взгляд на системы отсчета как на холст, на котором рисуются картины Природы, немедленно приводит к требованию, чтобы выбор холста не влиял на содержание картины. В частности, для этого необходимо, чтобы в механике использовались исключительно инвариантные дифференциальные операторы, т.е. операторы, не зависящие от выбора системы координат. Основными среди них являются операторы

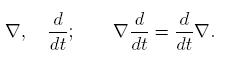
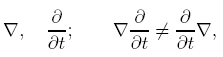
Формальная логика. В механике формальная логика не доводится до уровня математической строгости, но явные нарушения формальной логики считаются недопустимыми. В новейшей физике формальная логика объявлена предрассудком, а ее законы часто подменяются рассуждениями о красоте получаемых уравнений. П.Дирак пишет: “..мне бы хотелось подчеркнуть новую точку зрения, принадлежащую А.Эйнштейну. Он считал необходимым качеством фундаментальных уравнений присущую им красоту. Эйнштейн впервые высказал эту мысль и больше чем кто бы то ни было, подчеркивал важность красоты основных уравнений. Вы, конечно, можете спросить: почему уравнения должны обладать необыкновенной красотой? Я не могу ответить на это определенно. Можно лишь сказать, что этот принцип оказался чрезвычайно успешным”. В качестве примера нарушения логики сопоставим три утверждения одновременно принимаемые в физике: a) энергия E и импульс p сохраняются; b) масса m не сохраняется; c) справедливо равенство E =(m²c⁴ + p²c²)^1/2, где c - скорость света в пустоте, т.е. универсальная постоянная. Другой пример: перенормировка. П.Дирак пишет: “Таким образом, большинство физиков совершенно удовлетворены сложившейся ситуацией. Они считают, что квантовая электродинамика стала вполне совершенной теорией и о ней нечего больше беспокоиться. Должен сказать, что мне это в высшей степени не нравится, потому что в такой “совершенной” теории приходится пренебрегать в уравнениях бесконечностями, причем пренебрегать совершенно безосновательно. Это просто бессмысленно математически. В математике величину отбрасывают только в том случае, если она оказывается слишком малой, а не из-за того, что она бесконечно велика и от нее хотят избавиться!“. Для механиков отмечу, что перенормировка относится к числу важнейших принципов физики, а приведенные выше слова произнесены 15 сентября 1975г., т.е. относительно недавно и отнюдь не в первые годы существования квантовой физики. Отношение к формальной логике разделяет механику и новейшую физику трудно преодолимым барьером. Задачей механики является такое ее развитие, при котором известные в физике результаты получались бы без столь радикальных средств, как отказ от формальной логики.

Спинорные движения. В настоящее время уже многим понятно, что спинорные движения являются центральным звеном в устройстве мира. Это известно, по крайней мере, со времен Пифагора. Однако в рациональные науки спинорные движения были введены только Л.Эйлером, да и то не в полной мере. В механику спинорные движения начали интенсивно внедряться во второй половине XX века, причем указанное внедрение оказалось чрезвычайно естественным и органичным. Если внимательно изучать старые теории эфира, прекрасно описанные в книге Г.Лоренца, то бросается в глаза, что во всех этих теориях содержится попытка ввести спинорные движения. К сожалению, делается это неправильно. В то время единственным способом восприятия спинорного движения являлось представление о нем, как о роторе вектора скорости. На самом деле это не так. К обсуждению спинорных движений мы еще вернемся, а сейчас обратимся к новейшей физике. Строго говоря, спинорные движения в новейшей физике запрещены, но все-таки используются.

Г.Лоренц

П.Дирак приводит слова Г.Лоренца, адресованные авторам идеи наличия динамического спина у электрона голландским физикам Д.Уленбеку и С.Гоудсмиту,: “Нет, у электрона не может быть спина. Я и сам об этом думал, но если бы электрон вращался, то скорость на его поверхности превышала бы скорость света. Так что из этого ничего не выйдет”. Для механиков замечу, что хотя в современной физике используются термины “спин” и “магнитный момент” применительно к элементарным частицам, но они не имеют отношения к соответствующим понятиям механики: это просто красивые названия для номеров соответствующих гармоник у решений уравнений Шредингера или их обобщений. Если говорить о личном мнении, то я точно, хотя и на интуитивном уровне, знаю о колоссальной, ни с чем не сравнимой, роли спинорных движений в микромире. Атомная и ядерная энергии — это энергии спинорных движений. Специальная теория относительности запрещает спинорные движения, на что указал П.Эренфест сразу же после появления работы А.Эйнштейна 1905г. Но в таком случае СТО запрещает почти все, что на самом деле имеет место в Природе.

Экспериментальная проверка результатов теории. Все получаемые в механике результаты должны соответствовать данным эксперимента. Конечно, это трудно и есть немало экспериментов, результаты которых механика не может корректно описать в настоящее время. Например, ни одна теория пластичности не может правильно описать опыты Треска по экструзии свинца. Существует множество других проблем, не поддающихся в настоящее время теоретическому анализу. Но это не повод для того, чтобы кричать “караул” и выворачивать теорию наизнанку. В конце концов, для того и существует экспериментальная механика, чтобы решать проблемы, недоступные в настоящее время для теории. Так было, так есть и так всегда будет. Типичным для механики является эволюционный путь развития. В результате теория отстает от эксперимента на десятилетия и даже на столетия. Мне кажется, что это вполне нормально. Совершенно иначе проблему взаимоотношений между экспериментом и теорией решает новейшая физика. Ее формулы устроены таким образом, что позволяют почти автоматически объяснить все экспериментальные данные. Покажем, как это делается на примере. Допустим, мы хотим измерить скорость v_x частицы A. Введем штрихованную систему координат (излюбленный прием физиков), движущуюся со скоростью u = c - ε, где ε > 0 и пренебрежимо мала в сравнении со скоростью c = 3 10¹⁰ см/сек. Измерим теперь скорость v_x' частицы A в штрихованной системе. Допустим, что мы получили скорость v_x' = - c + η, где η > 0 малая величина, например η = 2 см/сек. Вычислим скорость v_x. Имеем по известной формуле

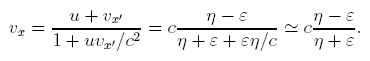
Приведенных примеров вполне достаточно, чтобы сделать вывод о том, что механика уже не является частью физики, как это было сто лет назад.

Следует подчеркнуть, что все сказанное ни в коем случае нельзя воспринимать как критику в адрес новейшей физики, ибо критика подразумевает анализ состояния дел в физике, чего выше нет и в помине. Да и о какой критике может идти речь? Как бы ни относиться к методам, используемым в современной физике, но невозможно отрицать тот очевидный факт, что физики еще десятки лет назад нашли правдоподобные ответы на такие вопросы, к решению которых механика только готовится приступить. Сумеет ли механика решить эти проблемы традиционными для нее методами? Это требует доказательств. Предстоит огромная работа. Цель данной работы в том и состоит, чтобы привлечь внимание механиков к решению фундаментальных проблем естествознания. Прежде всего, это относится к описанию явлений электромагнетизма и строения атома. Мне кажется, что механика способна внести свой вклад в эти важнейшие вопросы, которые, несмотря на все достижения физики, еще далеки от окончательных решений.