

 |
Elena A. Ivanova St. Petersburg State Polytechnical University |  |
Dynamics of ultracentrifuges
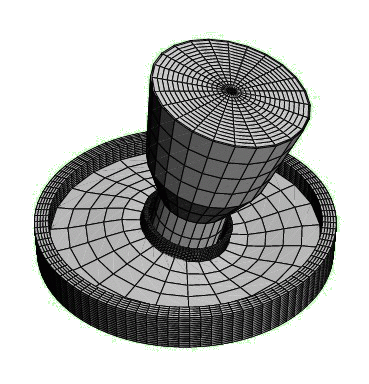 |
The mechanics problems, concerning to development of calculation methods for mechanical systems, including quickly rotating rotors on the elastic foundation, are rather numerous also many of them poorly studied from the theoretical point of view. Similar problems arise, in particular, in case of analysis of ultracentrifuges (centrifuges, which working angular velocity exceeds 100 thousand revolutions per minute), intended for super-clean separation of substances. Working frequencies of ultracentrifuges lay much above first eigenfrequencies of the system. Therefore the ultracentrifuge passes through some resonances during bringing and braking of the rotor. Thus the vibrations, accompanying with the big dynamic loadings, take place. Vibrations at a stage of braking are especially critical because they sharply reduce a level of the achieved clearing. As a rule, dynamic analysis of centrifuges is based on research of the models representing the rotating rigid body on the not inertial elastic foundation. Research of ultracentrifuges dynamics demands creation of more complex mechanical models which are taking into account properties of real designs in more detail. In particular, for creation of dynamic models of ultracentrifuges it is important to take into account inertial properties of the elastic foundation. |
Models of ultracentrifuges
The mechanical model of an ultracentrifuge is a rigid body on the elastic foundation. Continual model of the elastic foundation is represented as an inertial elastic plate in the form of a ring. The rigid body is supposed to be dynamically symmetric with small unbalance of mass. Nonlinear formulations of two problems of motion of a heavy rigid body on an inertial elastic plate are suggested. In the first problem the rigid body has the motionless point fixed with the help of the spherical hinge. In the second problem the rigid body has no motionless points. Both problems are reduced to systems of the scalar equations. The basic variables, describing kinematics of a rigid body and a plate, are chosen so that derived equations would be convenient for use in numerical procedures. Quasi-linear statements of problems have been investigated in detail. In particular, influence of various kinds of friction and the motor moments on the system motion stability has been investigated. It is established, that the following motor moment is optimum from considered moments, because at the action of following moment, motion of the system is stable for any ratio of friction coefficients. It is shown, that if the plate thickness is increased and simultaneously cross shear coefficient is decreased then oscillations amplitude of rigid body will decrease. Thus if in system there is a friction, damping free vibrations, the increase in stresses is insignificant. It is shown, that introduction to system of additional rotors gives possibility to brake rotating of a carrier body so that the total kinetic moment of the gyrostat is keeping constant. Use of additional rotors, rotating in the direction of rotation of carrier body, allows to essentially increase the second resonant frequency and to decrease the first one so the working range of angular velocities will be below the second resonant frequency. Use of an additional rotor, rotating in the opposite direction to the rotation of the carrier body, gives possibility to expand the range of up to resonant angular velocities. Results of researches can be found in papers:
 |
 |
 |
Development of the mathematical technique
Specificity of dynamics problems for the systems, consisting of the rotating rigid body and the inertial elastic foundation, is that the equations of motion of the rigid body are boundary conditions of a boundary-value problem. These problems belong to an intersection of two big divisions of mechanics: rigid body dynamics and solid mechanics. However, solving problems of such a kind it is necessary to use methods of solid mechanics for the description of motion both solids and rigid bodies. For the first time P.A.Zhilin has paid attention to this fact. Let us note, that a problem of the description of rigid body dynamics by using the methods of solid mechanics, arises not only at analysis of discrete - continual systems, but also at construction and analysis of models of non-classical continuous media, such as Kelvin's medium, which particles have rotational degrees of freedom. Thus, the obtained results can be applied in the area beyond subjects of the investigation. Development of the mathematical technique for rigid body dynamics, compatible with the mathematical technique used in solid mechanics, can be found in papers:
Author's summary of the Doctor of Science thesis
To view PDF files you can download free version of Adobe Acrobat Reader.